Optimization Algorithms and Game Theory

An optimization tool is developed specially for stability problems, which consists of optimization algorithms, geometry parametrization and mesh deformation, a dynamically updated surrogate model, design of experiments and a mode tracking scheme.

The real part of an eigenvalue represents the growth/decay rate of the corresponding eigenmode. When the real part of this eigenvalue is positive, the eigenmode is unstable and will grow through time, and vice versa. To minimize the growth rate of an unwanted eigenmode is regarded as an objective in the optimization, when this unwanted mode is unfavorable in the flow.

Genetic algorithm emulates the process of natural selection and genetic mechanism in Darwin’s theory of evolution, and seek the optimal solution through a natural genetic process. The genetic algorithm starts with an initial population (a set of potential solutions), which is consisted of a number of individuals with combinations of different genes. A gene is a member in a parameter array of an individual. By calling a cost function, the fitness of each individual is evaluated, and the best individuals are selected. After crossover and mutation of genes, new generations with higher fitness are obtained. After a certain amount of iterations, an optimal solution is reached.

NSGA-II

Non-dominated sorting genetic algorithm II is a fast and elitist multi-objective optimization algorithm, which uses an elitist principle, i.e. the elites of a population are given the opportunity to be carried to the next generation, and an explicit diversity preserving mechanism and emphasizes the non-dominated solutions. It gives globally Pareto-optimal set of parameters.

Game theory

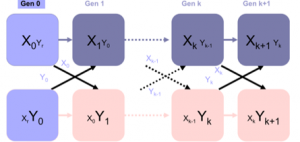Optimization and Game Theory have certain conceptual overlaps. In game theory, the Nash Equilibrium is “an action profile with the property that no single player can obtain a higher payoff by deviating unilaterally from this profile.” An equilibrium is reached since every player will conform to the decisions dictated by the profile. The optimization process of Nash Equilibrium is shown in figure 1.

Geometry Parametrization

For shape optimization, the geometry needs to be parameterized. The parameters representing the geometry are used and optimized in the optimization process to find the optimal shape. Super-elliptic functions are used for simple geometry representation, while CST and Hicks-Henne functions are used for a thorough representation of an airfoil. A super-elliptic curve is defined by the following form:

CST parametrization represents a two-dimensional geometry by the product of a class function, , and a shape function, , plus a term that characterizes the trailing edge thickness.

Hicks-Henne parametrization is composed by a series of Hick-Henne bump functions which are defined as:

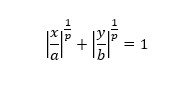
where p1 is the x location of the bump and p2 is the width of the bump.

Mesh Deformation

Since the shape optimization will deform the geometry, it is important to control the mesh deformation to avoid unusable meshes (e.g. with negative or distorted elements). To control the mesh deformation, a Free-form deformation (FFD) method is developed. The FFD acts on the two-dimensional boundary mesh deforming the inner grid, whilst maintaining the quality of the mesh.

Dynamically Updated Surrogate Model

Surrogate models are adopted in the process of optimization with complex cost functions, to reduce the calls of cost function evaluation, reducing the impact of uncertainty in evaluation and for easier parallel off-line evaluation, which is particularly important when considering expensive evaluations such as when considering base flow and stability analysis.

To ensure the accuracy of the surrogate model while reducing the computational cost in building the surrogate model, a dynamical update scheme is adopted. The surrogate model is updated with additional sample points each time when the optimization is converged, and then the optimization is restarted until the error between the surrogate model and the result from the actual analysis at the optimal point is below some criterion.

Design of Experiments

Design of experiments enables building surrogate models with minimal sampling of the cost functions. The most commonly employed experimental design methods are currently full factorial design, orthogonal design, uniform design, Latin hyper- cube sampling, central composite design, etc.

Mode Tracking Scheme

To include the stability analysis in the optimization loop, it is necessary to avoid manual identification of the eigenmodes obtained with new channel shape (i.e. identify the eigenmode responsible for the onset of asymmetry). A Modal Assurance Criterion (MAC) is incorporated into the optimization loop. The MAC method is an efficient way to track the modes by comparing sets of eigenmodes. To rank the similarity between eigenmodes, a MAC index is defined for a pair of eigenmodes (q_i ) ̂ and (q_j ) ̂:

Case 1: Contraction Channel

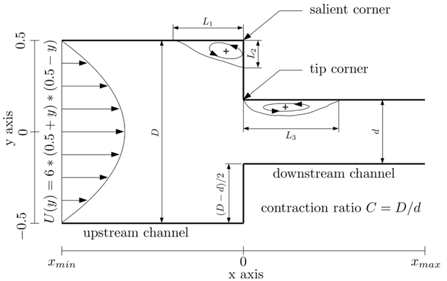
Problem description: In a contraction channel shown in figure 2, when the Reynolds number is increased above a critical value, the flow loses its symmetry. The asymmetry is caused by a asymmetric mode which optimization investigation is carried out to minimize its growth rate to make it stable. The optimization is modelled as:

in which, σ_R |_assym is the real part of the eigenvalue corresponds to the eigenmode that causes the asymmetry, p is the set of selected parameters defining the geometry, h_1 is the baseflow and h_2 represents the stability problem.

Results: The optimization finds an optimal shape with which the growth rate of the mode that causes the asymmetry below zero making this mode stable, detailed in figure 3.

Case 2: NACA0012

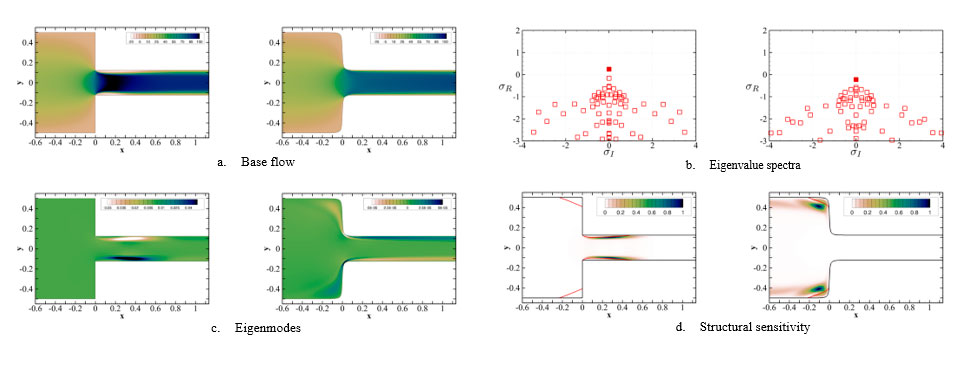
Problem description: In transonic flow conditions, the shock wave/turbulent boundary layer interaction and the flow separations on the upper wing surfaces of a civil aircraft induce flow instabilities, “buffet” and then structural vibrations, “buffeting”. In this case, we examine the flow around a NACA0012 airfoil, when the angle of attack is increased above a critical value, buffet phenomenon occurs. The eigenvalue spectra at different angle of attack and the eigenmode are shown in figure 4.

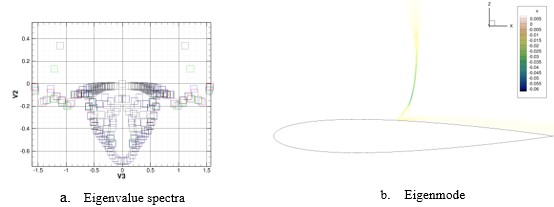
A multi-objective optimization investigation is conducted to minimize the growth rate of the mode that causes the buffet phenomenon and the drag. A bump is introduced on the airfoil near the area where the buffet phenomenon occurs. The optimization is modelled as:

in which, σ_R |_buf is the real part of the eigenvalue corresponds to the eigenmode that causes the buffet phenomenon, p is the set of selected parameters defining the geometry (location and size of the bump), h_1 is the baseflow and h_2 represents the stability problem. Nash equilibrium is adopted in this investigation.
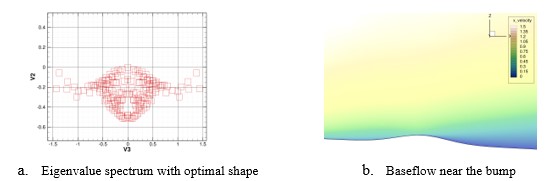
Results: The optimization finds an optimal combination of the size and the location of the bump that keeps the buffet phenomenon stable and minimizes the drag at the same time, shown in figure 5.