BiGlobal stability analysis uses a linearization of the Navier Stokes equations to extract the stability properties of a quasi-stationary two-dimensional flow. Using a Fourier transform on the third dimension, 2D and 3D periodic perturbations can be studied. The obtention of the eigenvalues and eigenvectors associated with such flow is reasonably cheap, costing much less than a full three dimensional DNS computation.

This method allows for a fast mapping of a parameter space, determining the neutral loops that separate the stable and unstable regimes.
Also, the eigenvectors and eigenvalues of the problem give information about characteristic of the leading perturbations, such as frequencies or critical dimensions, as well as sensitivity zones, information that can be applied to active or passive control.
The main problem studied by our group with this tool is the incompressible open cavity problem. Although the in the incompressible limit this problem is far from the industrial applications of aircraft landing gear or weapon bays, understanding the onset of the first structures over the laminar 2D flow is important.
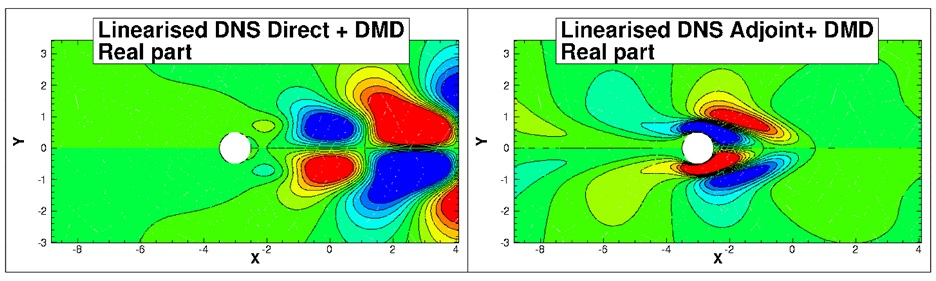
In other problem regimes there is no base state to use for linearization, but there are other techniques that can be used to analyze the stability properties of a flow in a saturated regime. In this cases, fluid flows can be approximated as a combination of infinite dynamic structures or modes that evolve in time.
These relevant structures can be extracted from the flow complexity and ranked by means of energy content (i.e. Proper Orthogonal Decomposition) or their time dynamics (i.e. frequency as in Dynamic Mode Decomposition). This snapshot type techniques (i.e. time-stepper) provide an alternative to the solution of large eigenvalue systems (i.e. matrix forming methods).
These type of approaches construct a Krylov subspace using snapshots issued from numerical simulations (or from experimental data). The resulting space can be subsequently analysed (e.g. Arnoldi technique or Dynamic Mode Decomposition) to obtain flow instability information related to the underlaying Navier-Stokes operator. These matrix free methods enable computations of the most unstable eigenvalues without requiring the solution of a complete eigenvalue system.





Copyright 2023 | Numath | Numerical Methods in aerospace technology | All rights reserved.
Terms and Conditions | Privacy Policy | Cookie Policy

