Research

Complex Systems

Our research line in complex systems science focuses both fundamental and applied questions in graph theoretical description of signals and dynamics, phase transitions and critical phenomena of systems, non-lineal dynamics and chaos, complex networks and complexity in living systems among others.

We have introduced the concept of visibility algorithms: methods to map time series to graphs, which we have been able to describe different types of dynamics in terms of associated graph features. The method has received wide attention and is currently investigated and used within several areas.

We have interest in social and biological problems showing collective phenomena and self-organization, such as animal search, social hierarchies, quantitative linguistics or ecological networks. Those systems and some other mathematics and physics problems shows emergent behavior that can be studied by the theory of complex systems.

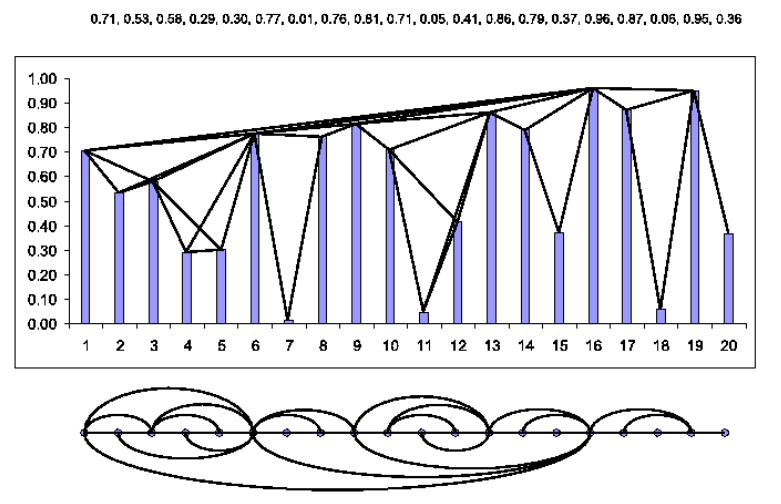
Figure 1
Is an example of a time series (20 data, depicted in the upper part) and the associated graph derived from the visibility algorithm.
In the graph, every node corresponds, in the same order to a series data. The visibility rays between the data define the links connecting nodes in the graph.

Figure 2
Shows the email contact network from one of our collaborator for 8 years. Each node is an email destination and the larger it is, means more contact has been maintained over time. The email network, like other complex network present small world properties and heavy tail degree distribution.