The advent of new powerful deep neural networks (DNNs) has fostered their application in a wide range of research areas, including more recently in fluid mechanics. In this presentation, we will cover some of the fundamentals of deep learning applied to computational fluid dynamics (CFD). Furthermore, we explore the capabilities of DNNs to perform various predictions in turbulent flows: we will use convolutional neural networks (CNNs) for non-intrusive sensing, i.e. to predict the flow in a turbulent open channel based on quantities measured at the wall. We show that it is possible to obtain very good flow predictions, outperforming traditional linear models, and we showcase the potential of transfer learning between friction Reynolds numbers of 180 and 550. We also discuss other modelling methods based on autoencoders (AEs) and generative adversarial networks (GANs), and we present results of deep-reinforcement-learning-based flow control.

Dr. Ricardo Vinuesa is an Associate Professor at the Department of Engineering Mechanics, at KTH Royal Institute of Technology in Stockholm. He is also a Researcher at the AI Sustainability Center in Stockholm and he acts as Vice Director of the KTH Digitalization Platform. He received his PhD in Mechanical and Aerospace Engineering from the Illinois Institute of Technology in Chicago. His research combines numerical simulations and data-driven methods to understand and model complex wall-bounded turbulent flows, such as the boundary layers developing around wings, obstacles, or the flow through ducted geometries. Dr. Vinuesa's research is funded by the Swedish Research Council (VR) and the Swedish e-Science Research Centre (SeRC). He has also received the Göran Gustafsson Award for Young Researchers.
Abstract
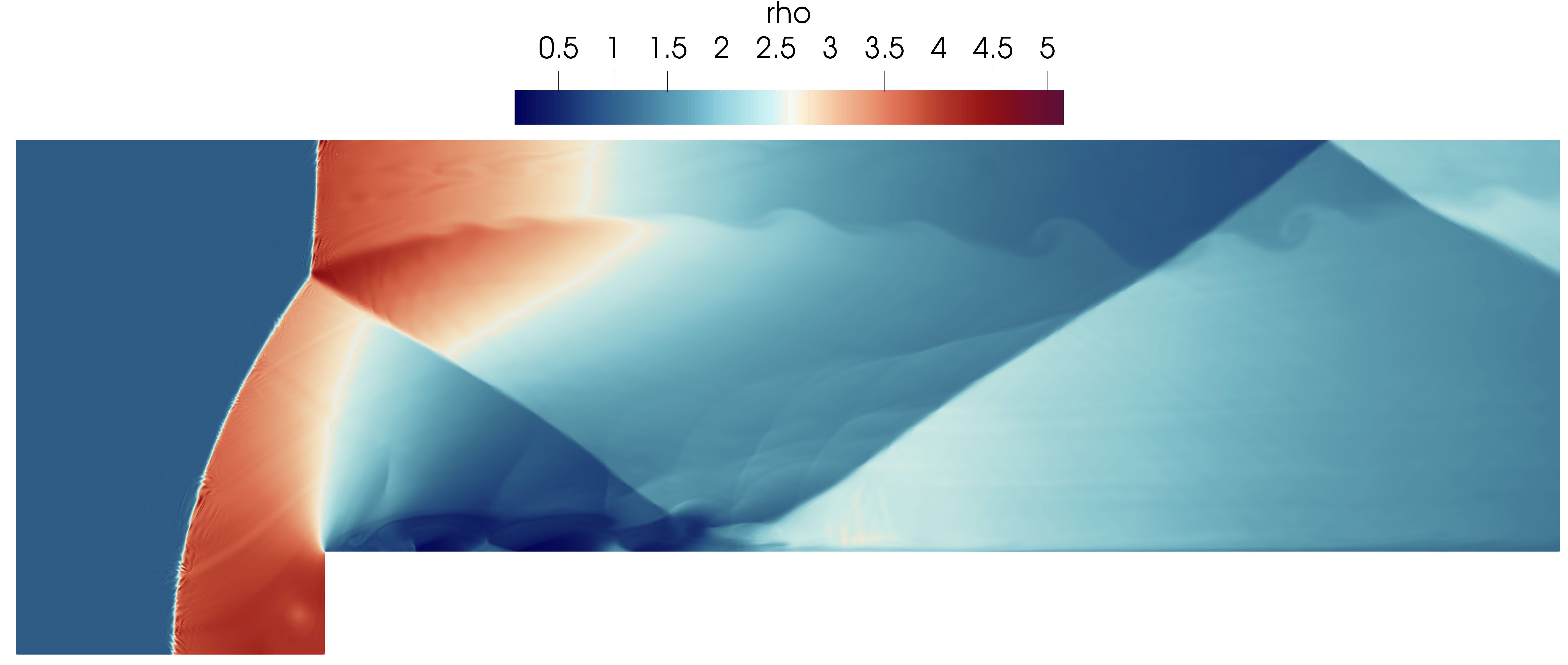
We propose an entropy-stable spectral vanishing viscosity (SVV) for discontinuous Galerkin discretizations, capable of adding the desired levels of dissipation in turbulent and supersonic flows. Within the SVV framework we enhance the dissipative fluxes, making them dependent on the solution amplitude for each wavenumber and, specifically, reducing their effect in low-frequency regions. This filtering makes use of an LDL decomposition of the fluxes that ensures the entropy-stability of the scheme when a proper formulation of the boundary conditions is applied. We also derive an entropy-stable approximation of the aforementioned SVV with Guermond–Popov fluxes and the Bassi–Rebay 1 scheme, which introduces density regularization in shock capturing applications.
This stabilization method is applied to the compressible Navier-Stokes equations with an additional artificial dissipation term, discretized with the Discontinuous Galerkin Spectral Element Method (DGSEM. To get an entropy-stable scheme, the new discrete terms are constructed to introduce a positive dissipation of the entropy as well. To this respect, we implement two different definitions of the artificial viscous flux. The first one increases the molecular viscosity of the fluid so that m = mv +ma. The second possibility, developed by Guermond and Popov, adds a viscous term in the density equation and propagates it to the momentum and energy equations, adding ma and aa as parameters that control the amount of viscosity added.
The artificial viscosity term is able to stabilize simulations with large gradients, such as shock-waves, by introducing dissipation controlled by the two parameters, ma and aa. However, to ensure that smooth regions are kept accurately resolved, we introduce two more steps in the algorithm. First, we use a sensor to find the shocked elements and second, we use a Spectral Vanishing Viscosity (SVV) by filtering the new term with a frequency dependent kernel, allowing us to control the amount of dissipation added in each mode.

Physicist with a PhD in Aerospace Engineering from the University of Stuttgart, with many years of experience in scientific software development and numerical simulation. Highly skilled in advanced numerical methods for partial differential equations, high-performance computing, and computational fluid dynamics, especially in the construction and development of robust and efficient parallel scientific codes based on very high-order conservative finite difference, finite volume, spectral difference, and discontinuous Galerkin spectral element methods, for solving the hydrodynamics, shallow water, Navier-Stokes, Maxwell, magnetohydrodynamics, relativistic hydrodynamics, and relativistic magnetohydrodynamics equations on structured and unstructured meshes.
Abstract
Elements composing complex systems usually interact in several different ways and as such the interaction architecture is well modelled by a network with multiple layers –a multiplex network–. However only in a few cases can such multi-layered architecture be empirically observed, as one usually only has experimental access to such structure from an aggregated projection. A fundamental challenge is thus to determine whether the hidden underlying architecture of complex systems is better modelled as a single interaction layer or results from the aggregation and interplay of multiple layers. Assuming a prior of intralayer Markovian diffusion, in this talk I will present a method [1] that, using local information provided by a random walker navigating the aggregated network, is able possible to determine in a robust manner whether these dynamics can be more accurately represented by a single layer or they are better explained by a (hidden) multiplex structure. In the latter case, I will also provide a Bayesian method to estimate the most probable number of hidden layers and the model parameters, thereby fully reconstructing its hidden architecture. The whole methodology enables to decipher the underlying multiplex architecture of complex systems by exploiting the non-Markovian signatures on the statistics of a single random walk on the aggregated network.
In fact, the mathematical formalism presented here extends above and beyond detection of physical layers in networked complex systems, as it provides a principled solution for the optimal decomposition and projection of complex, non-Markovian dynamics into a Markov switching combination of diffusive modes.
I will validate the proposed methodology with numerical simulations of both (i) random walks navigating hidden multiplex networks (thereby reconstructing the true hidden architecture) and (ii)
Markovian and non-Markovian continuous stochastic processes (thereby reconstructing an effective multiplex decomposition where each layer accounts for a different diffusive mode). I will also state two existence theorems guaranteeing that an exact reconstruction of the dynamics in terms of these hidden jump-Markov models is always possible for arbitrary finite-order Markovian and fully non-Markovian processes. Finally, using experiments, I will apply the methodology to understand the dynamics of RNA polymerases at the single-molecule level.
[1] L. Lacasa, I.P. Mariño, J. Miguez, V. Nicosia, E. Roldan, A. Lisica, S.W. Grill, J. Gómez-Gardeñes, Multiplex decomposition of non-Markovian dynamics and the hidden layer reconstruction problem, Physical Review X 8, 031038 (2018)
Abstract
This talk presents evidence of new scaling laws found in the human voice, originating at temporal scales below the phoneme, where the underlying mechanisms are not cognitive but only rely on the physiology of voice production.
We first show that during speech, the energy is unevenly released and power- law distributed, reporting a (language independent) Gutenberg–Richter-like law in speech. We further show that such ‘earthquakes in speech’ show temporal correlations and are invariant under a renormalization group transformation, suggesting that the process of voice production is indeed operating close to a critical point.
These results are put in contrast with current paradigms in speech processing, which usually invoke low dimensional deterministic chaos as the origin for nonlinear traits in microscopic voice fluctuations. As these latter fluctuations are indeed the aspects that humanize synthetic speech, these findings may have an impact in future speech synthesis technologies. Finally, we find that common linguistic laws reported in written texts (Zipf, Heaps and the brevity law) are already present in the microscopic fluctuations of voice. This suggests the provocative idea that the complexity of human communication might be after all just a byproduct of a complex physiological -rather than cognitive- system.

Dr. Lucas Lacasa studied Physics at Universidad Complutense and Technical University of Madrid, graduating with a PhD in Physics of Complex Systems in 2009. He has been an invited researcher at several universities including the University of Oxford and UCLA. He was an Assistant Professor at Technical University in Madrid (UPM) before moving to London in 2013 to accept a tenured position at the School of Mathematical Sciences, Queen Mary University of London (QMUL). At QMUL, he is a Reader in Applied Mathematics, as well as an EPSRC fellow and a visiting research fellow at King’s College London. At the end of 2021 he is moving back to Spain to take a tenured position at CSIC at the Institute for Cross-Disciplinary Physics in Complex Systems (IFISC) in Mallorca.
His research spans several areas of complexity science where he has published over 70 papers that have received over 4000 citations to date. Currently, he develops methods for data analysis and works at the interface of network theory and time series analysis, a topic for which he was awarded an EPSRC fellowship and has been recently awarded the international USERN prize in Formal Sciences.
The advent of new powerful deep neural networks (DNNs) has fostered their application in a wide range of research areas, including more recently in fluid mechanics. In this presentation, we will cover some of the fundamentals of deep learning applied to computational fluid dynamics (CFD). Furthermore, we explore the capabilities of DNNs to perform various predictions in turbulent flows: we will use convolutional neural networks (CNNs) for non-intrusive sensing, i.e. to predict the flow in a turbulent open channel based on quantities measured at the wall.
We show that it is possible to obtain very good flow predictions, outperforming traditional linear models, and we showcase the potential of transfer learning between friction Reynolds numbers of 180 and 550. These nonintrusive sensing models will play an important role in applications related to closed-loop control of wall-bounded turbulence. We also draw relevant connections between the development of AI and the achievement of the 17 Sustainable Development Goals of the United Nations.

Dr. Ricardo Vinuesa is an Associate Professor at the Department of Engineering Mechanics, at KTH Royal Institute of Technology in Stockholm. He is also a Researcher at the AI Sustainability Center in Stockholm and he acts as Vice Director of the KTH Digitalization Platform. He received his PhD in Mechanical and Aerospace Engineering from the Illinois Institute of Technology in Chicago. His research combines numerical simulations and data-driven methods to understand and model complex wall-bounded turbulent flows, such as the boundary layers developing around wings, obstacles, or the flow through ducted geometries. Dr. Vinuesa's research is funded by the Swedish Research Council (VR) and the Swedish e-Science Research Centre (SeRC). He has also received the Göran Gustafsson Award for Young Researchers.





Copyright 2023 | Numath | Numerical Methods in aerospace technology | All rights reserved.
Terms and Conditions | Privacy Policy | Cookie Policy

