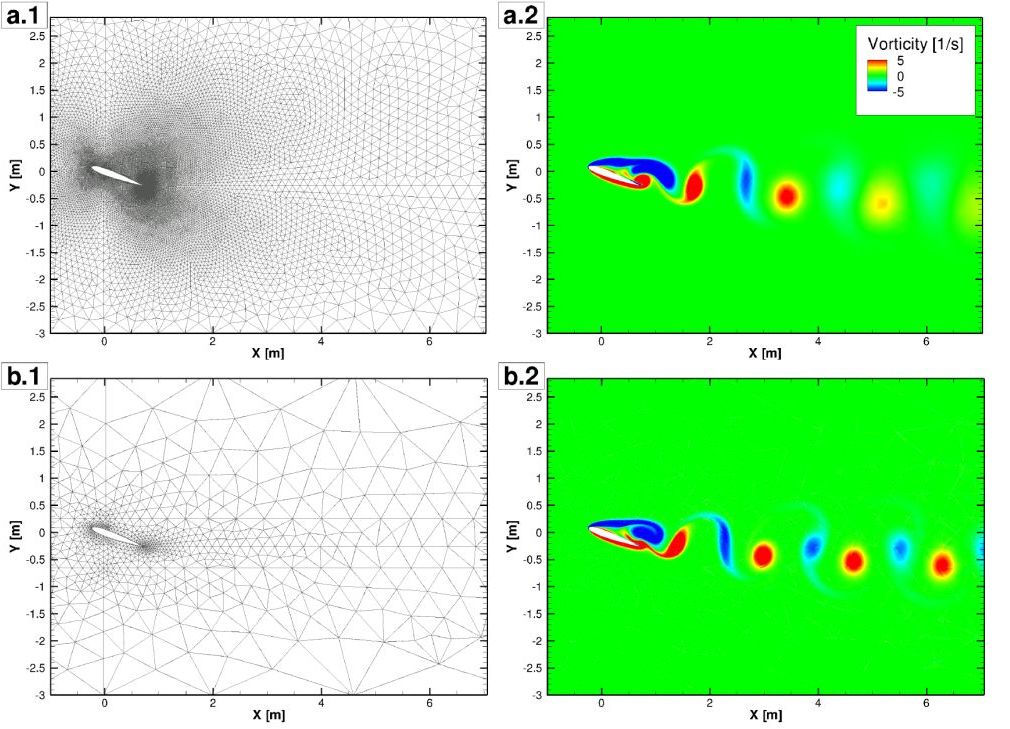
Our field of expertise in high order methods includes pure spectral methods, hp spectral element methods and high order DG methods (both nodal, and modal).
High order methods are the natural evolution of low order methods and they beat them in accuracy per degree of freedom, numerical dissipation and suitability for new hardware paradigm.
The simulation community has been using for decades traditional or low order methods. In fact, the numerical core of actual simulation tools relies in low order methods such as Finite Differences, Finite Volumes, and low order Finite Elements methods.
High order methods have been used in the academic community for a long time. The main difference between low and high order methods is that, while low order methods can only rely on mesh refinement (i.e. h-refinement) to obtain more accurate solutions, high order methods allow for mesh and polynomial refinement (i.e. p-refinement) strategies. This last path to obtain better accuracy considers a mesh with a fixed number of elements where the polynomial order within each element is increased, leading to a better approximation of the exact solution for smooth problems.
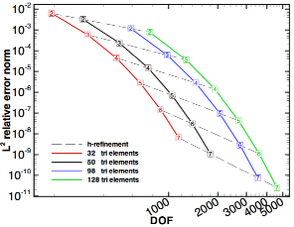
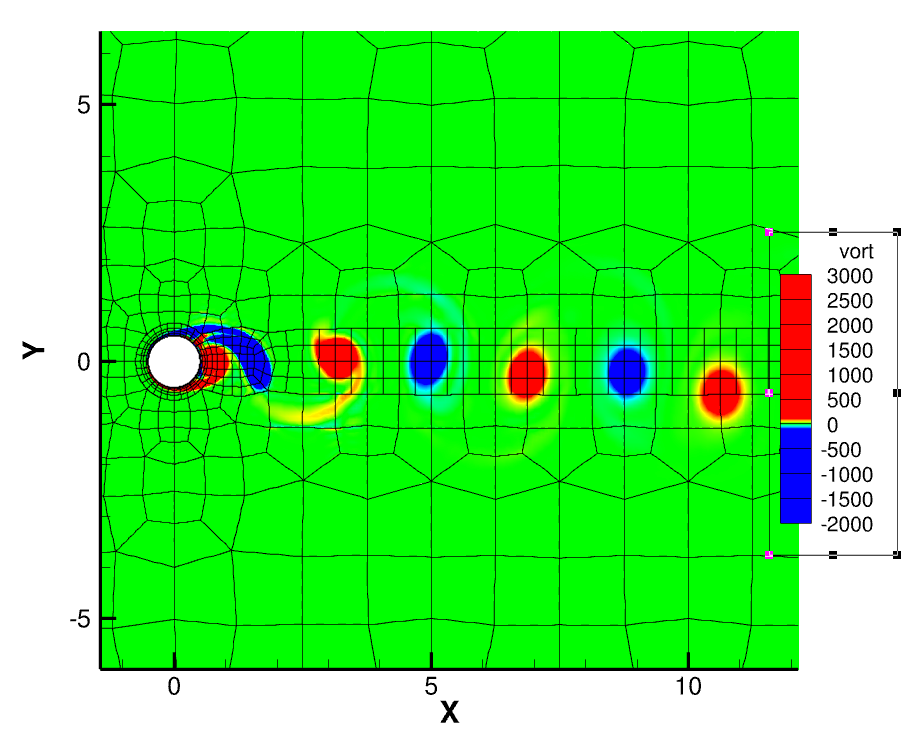
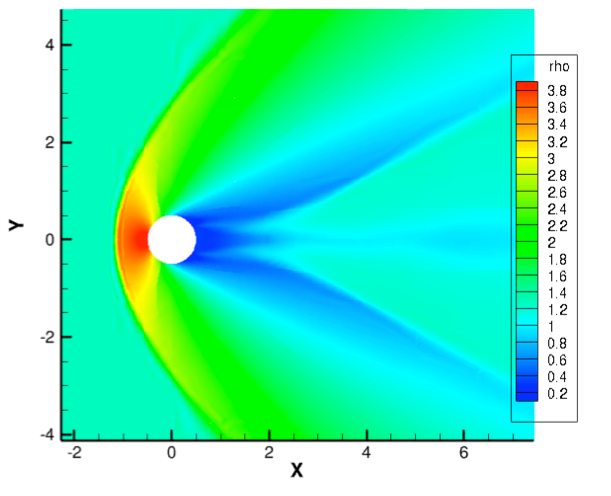
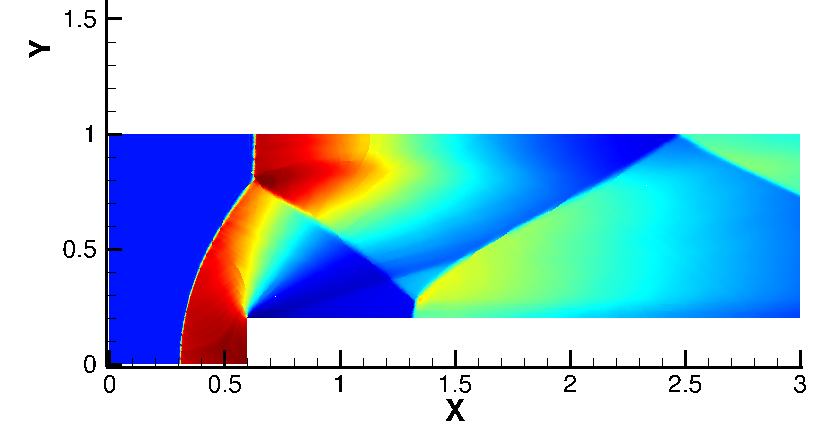
We show the effect of h- or p- refinement in the accuracy of the solution. As can be seen, High order methods permits a much more effective refinement process.
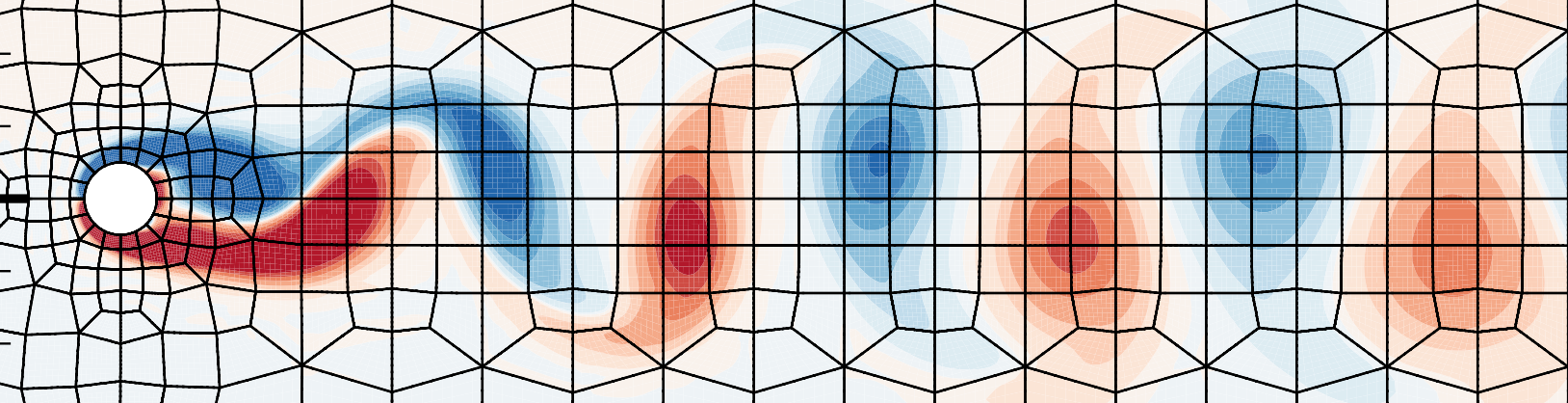





Copyright 2023 | Numath | Numerical Methods in aerospace technology | All rights reserved.
Terms and Conditions | Privacy Policy | Cookie Policy

