Horses3D

Overview

HORSES3D is a 3D parallel code that uses the high–order Discontinuous Galerkin Spectral Element Method (DGSEM) and is written in modern object–oriented Fortran (2008+), see Ferrer et al. [2020]

The code is currently being developed at ETSIAE–UPM (the School of Aeronautics of the Universidad Politécnica de Madrid). HORSES3D is built on the NSLITE3D code by David A. Kopriva, which is based on the book “Implementing Spectral Methods for Partial Differential Equations” Kopriva [2009].

HORSES3D provides the following features:

Hybrid (shared and distributed memory) CPU–based parallelization with OpenMP and MPI.
A multiphysics environment where the compressible Euler equations of gas dynamics, the compressible Navier–Stokes equations, the incompressible Navier–Stokes equations with artificial compressibility Shen [1997], the Cahn– Hilliard equation, and the entropy–stable two–phases solver are implemented.
Implementations of the split–form DGSEM.
Support for arbitrary high–order, p–anisotropic discretizations.
Implicit time integration schemes such as the Backward Differentiation Formulas (BDFs) and the Rosenbrock type implicit Runge–Kutta methods.

Multiple linear solvers for the implicit time–integration schemes: a preconditioned matrix–free GMRES solver, a direct LU solver (the implementation of PARDISO that is present in Intel’s Math Kernel Library –MKL), a matrix–based GMRES solver (from the PETSc library Balay et al. [2019]) and static–condensation methods.
Numerical Jacobian computations with a coloring algorithm.
Analytical Jacobian computations for nonlinear advection and/or diffusion systems of conservation laws.
Nonlinear multigrid techniques with explicit (Runge–Kutta schemes) and implicit (BDF + iterative methods) smoothers. Two cycling stratefies are implemented: Full Multigrid (FMG) and V–Cycling.
Support for curvilinear, hexahedral, conforming meshes in SpecMesh/HOHQMesh format (*.mesh) and HOPR Hindenlang et al. [2015] format (*.h5).
Static and dynamic p–adaptation methods for steady and unsteady simulations that use p–anisotropic truncation error estimates.

Numath-Tools-Horses-Fig.4 — Figure 4 Multiphase solver. Evolution of the physical mode that configures an annular flow in a pipe. We have represented fluid 2 (i.e. c < 0.5), colored with vertical velocity, u. We see that during early times, there is an unstable physical mode that triggers the annular flow. When fluid 2 rises above the interface, it is dragged and accelerated by the quicker fluid 1. When it is confined below the interface, it is slowed down by the wall. This evolves non-linearly to the final state.

Physics implemented

HORSES3D uses a nodal Discontinuous Galerkin (DG) Spectral Element Method (DGSEM) for the discretization of the different physics implemented. In particular, it permits the use of the Gauss–Lobatto version of the DGSEM, which makes it possible to construct energy–stable schemes using the summation–by–parts simultaneous–aproximation– term (SBP–SAT) property. Moreover, it handles arbitrary three dimensional curvilinear hexahedral meshes while maintaining high–order spectral accuracy and free–energy stability.

Compressible Navier Stokes

HORSES3D was originally developed to solve the compressible Navier Stokes equations. This set of equations permits the simulation of plenty of phenomena of scientific and engineering interest (aerodynamics, weather predictions, confined flows…). However, HORSES3D also incorporates nonstandard physical models that are described below.

Incompressible Navier Stokes

Among the different incompressible NSE models, HORSES3D uses the artificial compressibility method Shen [1997], which converts the elliptic problem into a hyperbolic system of equations, at the expense of a non divergence–free velocity field. However, it allows one to avoid constructing an approximation that satisfies the inf–sup condition Karniadakis and Sherwin [1999]; Ferrer [2017]. The artificial compressibility model is commonly combined with dual time–stepping, which solves an inner pseudo–time step loop until velocity divergence errors are lower than a selected threshold, then performs the physical time marching Cox et al. [2016]. For a detailed explanation of the model see J. Manzanero, G. Rubio, D. A. Kopriva, E. Ferrer, E. Valero, Entropy-stable discontinuous Galerkin approximation with summation-by-parts property for the incompressible Navier-Stokes equations with variable density and artificial compressibility, arXiv preprint arXiv:1907.05976 .

Cahn Hilliard

Phase field models describe the phase separation dynamics of two immiscible liquids by minimizing a chosen free–energy. For an arbitrary free–energy function, it is possible to construct different phase field models. Among the most popular, one can find the Cahn–Hilliard Cahn and Hilliard [1958] and the Allen–Cahn Allen and Cahn [1972] models. The popularity of the first, despite being a fourth order operator in space, comes from its ability to conserve the phases. HORSES3D permits the solution of the Cahn-Hilliard equation. For a detailed explanation of the model see J. Manzanero, G. Rubio, D. A. Kopriva, E. Ferrer, E. Valero, A free–energy stable nodal discontinuous Galerkin approximation with summation–by–parts property for the Cahn–Hilliard equation, Journal of Computational Physics 403 (2020a) 109072.

Multiphase flow (Cahn Hilliard + Incompressible Navier Stokes)

The multiphase flow solver implemented in HORSES3D is constructed by a combination of the the diffuse interface model of Cahn–Hilliard Cahn and Hilliard [1958, 1959] with the incompressible Navier–Stokes equations with variable density and artificial (also called pseudo) compressibility Shen [1996]. This model guarantees the mass conservation with an accurate representation of surface tension effects. For a detailed explanation of the model see J. Manzanero, G. Rubio, D. A. Kopriva, E. Ferrer, E. Valero, Entropy-stable discontinuous Galerkin approximation with summation-by-parts property for the incompressible Navier-Stokes/Cahn-Hilliard system, arXiv preprint arXiv:1910.11252 .

Scalability

The code is equipped with distributed memory parallelization using MPI, and shared memory parallelization using OpenMP. In this section, we present strong scalability tests for HORSES3D.

Shared Memory (OpenMP)

The shared–memory parallelization distributes the most expensive tasks (i.e. the volume and surface integral computations) to different threads using OpenMP directives.

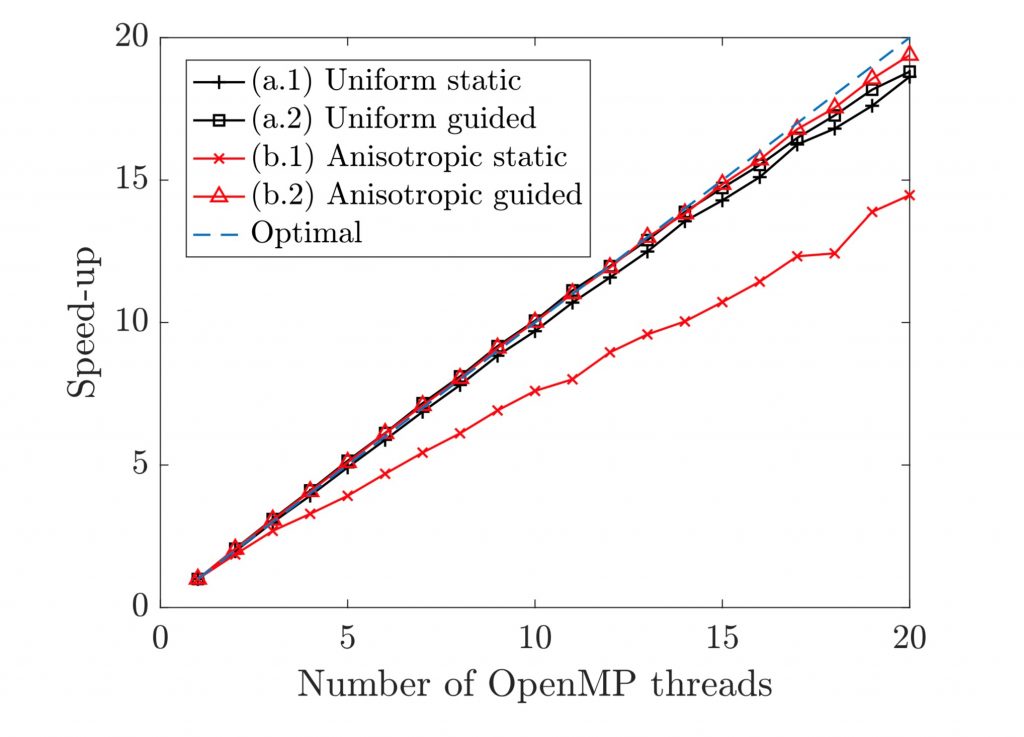
In this section, a strong scalability test is presented for the flow around a sphere (the details can be found in Rueda-Ramírez [2019]). Roe is used as the inviscid Riemann Solver and the BR1 scheme for the viscous boundary terms.

Two common OpenMP schedules were tested: static and guided. The static schedule divides the loops of elements and faces into equal–sized chunks (or as equal as possible) for the different available threads, i.e.

chunk_size = num_of_elements/num_of_threads, (1) and chunk_size = num_of_faces/num_of_threads, (2)

respectively. The guided schedule gives a smaller chunk of loop iterations to each thread. When a thread finishes, it retrieves another chunk to compute. The chunk size starts large and decreases as the loop computation is completed.

The computation time needed for taking 100 time steps (RK3) was measured using a 2–socket Intel CPU with 2×20 cores at 2.2GHz and 529 GB RAM. Two discretizations with roughly the same number of DOFs (±5%) were used:

A uniform order (N1 = N2 = N3 = 5) discretization (411264 DOFs).
The p–anisotropicdiscretizationthatwasobtainedwithaτ–basedp–adaptation procedure, which provided an improved accuracy (comparable to the N = Nmax = 7 discretization) for a similar number of degrees of freedom (431667 DOFs). The interested reader can find more details in Rueda-Ramírez et al. [2019a,c]

Each of the simulations was run five times and the computation time was averaged. The results are shown in Figure 5.

As can be seen in Figure B.1, the code has a near–optimal scalability when using OpenMP + guided schedule. Only the anisotropically p–adapted discretization performs suboptimally when the OpenMP schedule is static. However, in OpenMP the guided schedule provides an efficient load balancing.

Distributed Memory (MPI/OpenMP+MPI)

The benchmark solved herein is the inviscid Taylor–Green Vortex (TGV) problem. We consider a coarse mesh with 32³, and a fine mesh with 64³ elements, and we vary the polynomial order from N = 3 to N = 6. The solver scalability curves are depicted in Figures 6 and 7. We consider both pure MPI, and Hybrid (OpenMP+MPI) strategies. The number of total cores ranges from 1 to 700, and the number of OpenMP threads, when enabled, is 48.

The 32³ mesh, using MPI (Fig. 6) does not show an increase in the solver speed–up when increasing the number of cores. Since this mesh is coarse (81 elements per core when using 400 cores, 54 elements per core when using 600), it seems normal that communication time is the bottleneck in this simulation. However, with this configuration it is possible to obtain speed–ups of 100 using 100 cores, depending on the polynomial order. The Hybrid strategy (Fig. 6), on the other hand, is capable to maintain high speed–ups before the stagnation, approximately on 500 cores. The higher the polynomial order, the higher the speed–up since more calculations inside the elements are performed (i.e. they do not involve communication).

The medium mesh is represented in Fig. 7. Regarding the MPI strategy, Fig. 7, we observe an improvement when compared to the coarser mesh in Fig. 6.
We do not observe stagnation for high polynomial orders, and in the rest, the stagnation occurs after using approximately 400 cores. The Hybrid strategy in Fig. 7 does not show stagnation in the range considered. Despite being slighly irregular for lower polynomial orders, a straight line is achieved with N = 6.

Getting the Code

If you wish to just use Horses3D for running simulations, we recommend downloading a pre-compiled binary distribution package for your distribution from the Downloads page.

If you plan to develop new code or extend the existing functionality, or would just prefer to compile it yourself, there are three ways to get the code

The code is available in GitHub: https://github.com/loganoz/horses3d

Bibliography

Allen, S. M., & Cahn, J. W. (1972). Ground state structures in ordered binary alloys with second neighbor interactions. Acta Metallurgica, 20(3), 423-433.

Balay, S. Abhyankar, M. Adams, J. Brown, P. Brune, K. Buschelman, L. Dalcin, A. Dener, V. Eijkhout, W. Gropp, et al., PETSc users manual.

Cahn, J. W., & Hilliard, J. E. (1958). Free energy of a nonuniform system. I. Interfacial free energy. The Journal of chemical physics, 28(2), 258-267.

Cahn, J. W., & Hilliard, J. E. (1959). Free energy of a nonuniform system. III. Nucleation in a two‐component incompressible fluid. The Journal of chemical physics, 31(3), 688-699.

Cox, C., Liang, C., & Plesniak, M. W. (2016). A high-order solver for unsteady incompressible Navier–Stokes equations using the flux reconstruction method on unstructured grids with implicit dual time stepping. Journal of Computational Physics, 314, 414-435.

Ferrer, E. (2017). An interior penalty stabilised incompressible discontinuous Galerkin–Fourier solver for implicit large eddy simulations. Journal of Computational Physics, 348, 754-775.

Hindenlang, F., Bolemann, T., & Munz, C. D. (2015). Mesh curving techniques for high order discontinuous Galerkin simulations. In IDIHOM: Industrialization of high-order methods-a top-down approach (pp. 133-152). Springer, Cham.

Karniadakis, G., & Sherwin, S. (2013). Spectral/hp element methods for computational fluid dynamics. Oxford University Press.

Kopriva, D. A. (2009). Implementing spectral methods for partial differential equations: Algorithms for scientists and engineers. Springer Science & Business Media.

Manzanero, J., Rubio, G., Kopriva, D. A., Ferrer, E., & Valero, E. (2020). A free–energy stable nodal discontinuous Galerkin approximation with summation–by–parts property for the Cahn–Hilliard equation. Journal of Computational Physics, 403, 109072.

Manzanero, J., Rubio, G., Kopriva, D. A., Ferrer, E., & Valero, E. (2020). An entropy–stable discontinuous Galerkin approximation for the incompressible Navier–Stokes equations with variable density and artificial compressibility. Journal of Computational Physics, 408, 109241.

Manzanero, J., Rubio, G., Kopriva, D. A., Ferrer, E., & Valero, E. (2020). Entropy–stable discontinuous Galerkin approximation with summation–by–parts property for the incompressible Navier–Stokes/Cahn–Hilliard system. Journal of Computational Physics, 109363.

Manzanero, J., Ferrer, E., Rubio, G., & Valero, E. (2020). Design of a Smagorinsky Spectral Vanishing Viscosity turbulence model for discontinuous Galerkin methods. Computers & Fluids, 104440.

Rueda-Ramírez, A. M., Rubio, G., Ferrer, E., & Valero, E. (2019). Truncation Error Estimation in the p-Anisotropic Discontinuous Galerkin Spectral Element Method. Journal of Scientific Computing, 78(1), 433-466.

Rueda-Ramírez, A. M., Manzanero, J., Ferrer, E., Rubio, G., & Valero, E. (2019). A p-multigrid strategy with anisotropic p-adaptation based on truncation errors for high-order discontinuous Galerkin methods. Journal of Computational Physics, 378, 209-233.

Rueda-Ramírez, A. M. (2019). Efficient Space and Time Solution Techniques for High-Order Discontinuous Galerkin Discretizations of the 3D Compressible Navier-Stokes Equations(Doctoral dissertation, Universidad Politécnica de Madrid).

Shen, J. (1996). On a new pseudocompressibility method for the incompressible Navier-Stokes equations. Applied numerical mathematics, 21(1), 71-90.

E Ferrer, G Rubio, G Ntoukas, W Laskowski, OA Mariño, S Colombo, A Mateo-Gabín, F Manrique de Lara, D Huergo, J Manzanero, AM Rueda-Ramírez, DA Kopriva, E Valero (2022). HORSES3D: a high-order discontinuous Galerkin solver for flow simulations and multi-physics applications. arXiv preprint arXiv:2206.09733